MathGenius Pro – AI-Powered Math Solver Using Python

Introduction:

From simple arithmetic to more complicated college-level subjects like integration, differentiation, algebra, matrices, and graph plotting, MathGenius Pro is a clever, Python-based math solver made to tackle a broad range of mathematical problems. It provides quick, precise answers by utilizing strong AI and symbolic computation libraries (such as SymPy). This project’s primary goal is to make math problems easier for teachers, students, and self-learners to solve and comprehend. MathGenius Pro is an excellent learning tool because, in contrast to standard calculators, it provides step-by-step instructions.

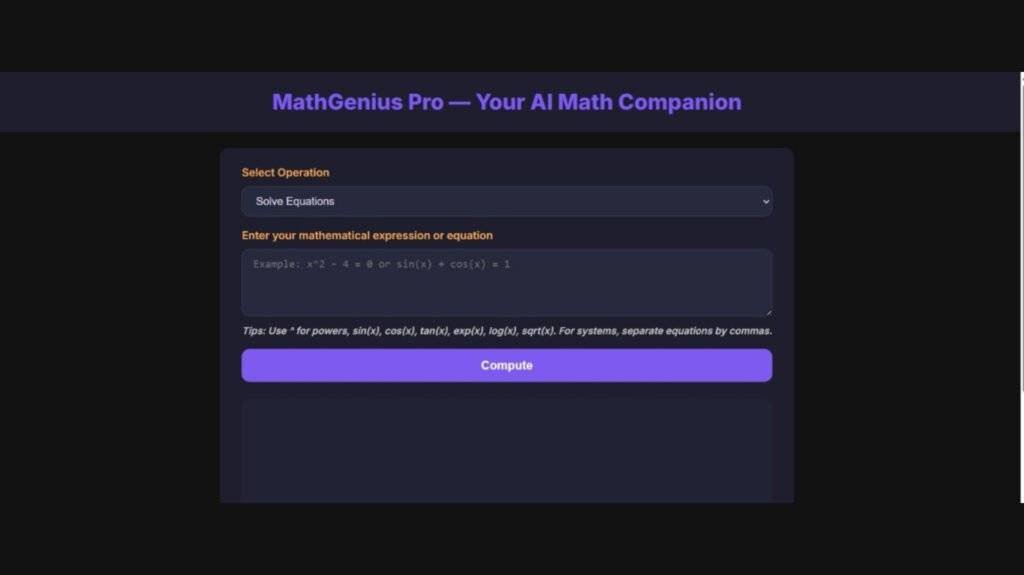
Users can type or choose the kind of problem they wish to solve in the application’s clear, intuitive graphical user interface. After receiving input, the AI engine analyzes the issue and presents the solution along with a detailed explanation. Plots and graphs are also displayed when appropriate.

Key features include:

Step-by-step solving of equations
Symbolic differentiation & integration
Matrix operations
Graph plotting of functions
Natural language input support (optional via NLP)

MathGenius Pro is special because it combines intelligent AI problem-solving, informative feedback, and an eye-catching user interface to make math interesting and approachable.

Required Modules Or Packages:

Streamlit – It will Enables in building interactive and beautiful web apps by using Python.
Sympy – It is a symbolic mathematics library of python which is used for algebra, calculus, and equation solving.
parse_expr (from sympy.parsing.sympy_parser) – It will Converts the string inputs into symbolic math expressions.
NumPy – It is used for providing support for numerical operations and handling of arrays.
plotly.graph_objs – It is Used for creating interactive graphs and plots.
Pyttsx3 – It will Allows text-to-speech conversion offline using Python.
Time – It will Provides the functions for tracking and managing time delays and timestamps.
Threading – It will Enables the running multiple operations concurrently by using threads.

To install these Packages, use the following command:

1. Streamlit (for UI):

pip install streamlit

2. SymPy (for symbolic math like integration/differentiation):

pip install sympy

3. NumPy (for numerical operations):

pip install numpy

4. Plotly (for interactive graphs and plots):

pip install plotly

5. pyttsx3 (for offline text-to-speech output):

pip install pyttsx3

How To Run The Code:

Method 1:

Step 1 . First , You Download and Install Visual Studio Code or VS Code In your PC or Laptop by VS Code Official Website .

Step 2 . Now Open CMD As Administrator and install the above packages using Pip .

Step 3 . Now Open Visual Studio Code .

Step 4. Now Make The file named as main.py .

Step 5 . Now Copy And Paste The Code from the Link Given Below ⬇️

Step 6 . After pasting The Code , Save This & Click On Run Button .

Step 7 . Now You will See The Output .

Method 2:

Step 1 . First , You Download and Install Visual Studio Code or VS Code In your PC or Laptop by VS Code Official Website .

Step 2 . Now Open CMD As Administrator and install the above packages using Pip .

Step 3 . Now Open the link , which is provided below.

Step 4. Now download the ZIP file of the code.

Step 5 . Now Extract the ZIP file and Open in VS Code.

Step 6 . Now go to the main file and click on run button.

Step 7 . Now You will See The Output .

Code Explanation:

This Python code is used to Create an MathGenius Pro – An AI-Powered Math Solver. Ensures that You Have Downloaded the modules given above .

Importing Required Libraries:

import streamlit as st
import sympy as sp
from sympy.parsing.sympy_parser import parse_expr
import numpy as np
import plotly.graph_objs as go
import pyttsx3
import time
import threading

Streamlit – It will Enables in building interactive and beautiful web apps by using Python.
Sympy – It is a symbolic mathematics library of python which is used for algebra, calculus, and equation solving.
parse_expr (from sympy.parsing.sympy_parser) – It will Converts the string inputs into symbolic math expressions.
NumPy – It is used for providing support for numerical operations and handling of arrays.
plotly.graph_objs – It is Used for creating interactive graphs and plots.
Pyttsx3 – It will Allows text-to-speech conversion offline using Python.
Time – It will Provides the functions for tracking and managing time delays and timestamps.
Threading – It will Enables the running multiple operations concurrently by using threads.

🔹 1. Text-to-Speech Integration:

engine = pyttsx3.init()
...
def speak(text: str):
if engine:
threading.Thread(target=lambda: engine.say(text) or engine.runAndWait()).start()

This part will initializes the pyttsx3 engine for offline text-to-speech feature. The speak() function will uses the threading to avoid the blocking of UI. It will reads the output aloud, also used in enhancing accessibility and user experience.

🔹 2. Streamlit Configuration and Styling:

st.set_page_config(...)
...
st.markdown(f"<style>{dark_css}</style>", unsafe_allow_html=True)

This section of the code will sets up the Streamlit app’s layout, page title, and dark-themed custom UI. It will ensures a clean, modern, and user-friendly interface with styled buttons, inputs, and headers, making the app readable.

🔹 3. Expression Parsing:

def parse_math_expression(expr_str, locals_dict={}):
expr = parse_expr(expr_str, local_dict=locals_dict, evaluate=True)
return expr

This function in this code will converts the string input (like “x^2 + 2*x + 1”) into a symbolic SymPy expression, which can then be manipulated mathematically (e.g., differentiated or integrated).

🔹 4. Equation Solver:

def solve_equation(input_text):
...
solutions = sp.solve(eq, syms, dict=True)

This is one of the core features in this app. It will handles both the single equations and the systems (separated by , or ;). It supports all the algebraic, trigonometric, exponential, and logarithmic equations by solving them by using SymPy’s solve() function.

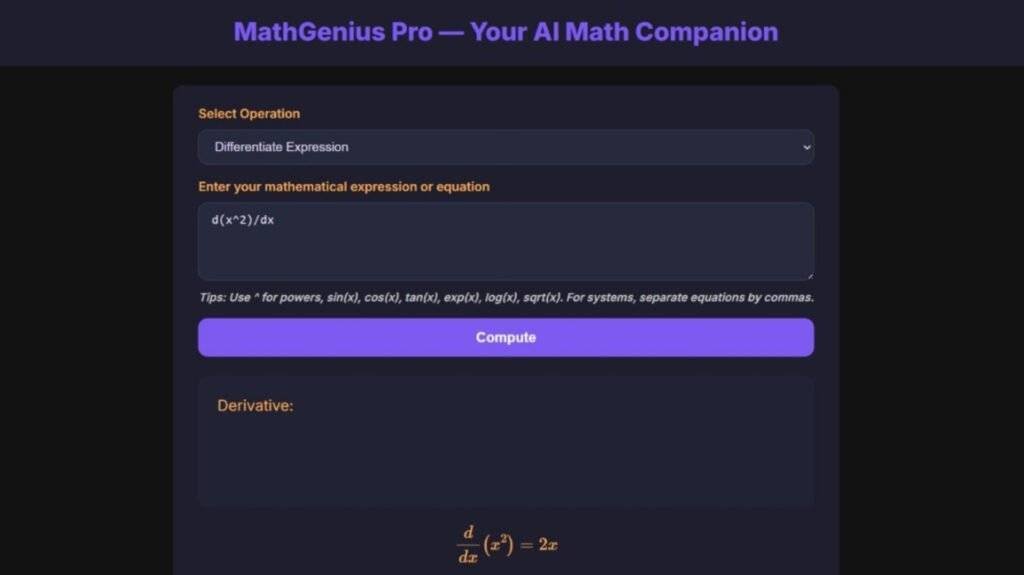
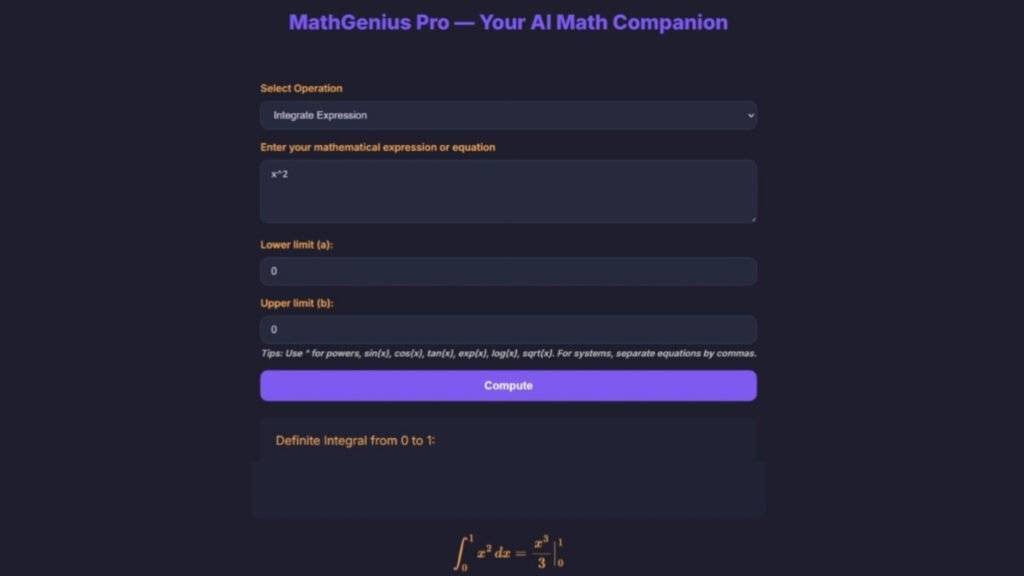
🔹 5. Differentiation & Integration:

def differentiate_expression(expr_str):
...
return sp.diff(expr, x)
def integrate_expression(expr_str, definite=False, lower=None, upper=None):
...
return sp.integrate(expr, (x, lower, upper)) if definite else sp.integrate(expr, x)

These functions in this code will allow the user to perform symbolic differentiation and integration. In this App, Users can choose between definite and indefinite integrals, and results are shown in LaTeX format.

🔹 6. Plotting Mathematical Functions:

def create_plot(expr_str):
...
fig = go.Figure()
fig.add_trace(go.Scatter(...))

This block of the code will generates an interactive graph using plotly. It parses the user’s expression, then converts it into a numerical function using lambdify, and after that plots it over a range of x-values (from -10 to 10).

🔹 7. User Interface and Flow Control:

def main():
...
operation = st.sidebar.selectbox(...)
expr_input = st.text_area(...)

This block of the code is the main user interaction logic. It is Based on the user selections (like solve, differentiate, integrate, plot), the app will routes to the relevant function and then displays the result.

🔹 8. Landing Page Animation:

def landing_page():
...
st.experimental_rerun()

The animated welcome screen adds a professional and engaging start to the app. It uses CSS keyframes for smooth fade-in and slide-up effects, which is creating a dynamic user experience.

Source Code:

				
					import streamlit as st
import sympy as sp
from sympy.parsing.sympy_parser import parse_expr
import numpy as np
import plotly.graph_objs as go
import pyttsx3
import time
import threading

# Initialize text-to-speech engine (optional)
try:
    engine = pyttsx3.init()
except Exception:
    engine = None

def speak(text: str):
    if engine:
        threading.Thread(target=lambda: engine.say(text) or engine.runAndWait()).start()

# Streamlit page configs
st.set_page_config(
    page_title="MathGenius Pro",
    layout="wide",
    initial_sidebar_state="expanded",
    page_icon="🧮"
)

# CSS for dark theme and custom styling
dark_css = """
    :root {
      --primary-color: #7f5af0;
      --background-color: #121212;
      --card-bg: #1e1e2f;
      --text-color: #e0def4;
      --accent-color: #f6ad55;
      --error-color: #f56565;
      --border-radius: 12px;
    }

    body, .css-1d391kg {
      background-color: var(--background-color);
      color: var(--text-color);
      font-family: 'Inter', sans-serif;
      line-height: 1.5;
    }
    /* Sidebar styling */
    section[data-testid="stSidebar"] {
      background-color: var(--card-bg);
      border-radius: var(--border-radius);
      padding: 24px 16px 32px 24px;
    }
    /* Header */
    header.css-18e3th9 {
      background: var(--card-bg);
      border-radius: var(--border-radius);
      padding: 16px 24px;
      font-weight: 600;
      font-size: 1.4rem;
      color: var(--primary-color);
      text-align: center;
      user-select: none;
      margin-bottom: 24px;
    }
    /* Cards */
    .stButton &gt; button {
      background-color: var(--primary-color);
      color: white;
      font-weight: 600;
      padding: 12px 24px;
      border-radius: var(--border-radius);
      border: none;
      transition: background-color 0.3s ease;
      width: 100%;
    }
    .stButton &gt; button:hover {
      background-color: #6c4ee3;
    }
    /* Inputs */
    .stTextInput&gt;div&gt;div&gt;input {
      background-color: #27293d;
      color: var(--text-color);
      border-radius: var(--border-radius);
      border: 1px solid #44455a;
      padding: 12px 16px;
      font-size: 1rem;
      transition: border-color 0.3s ease;
    }
    .stTextInput&gt;div&gt;div&gt;input:focus {
      outline: none;
      border-color: var(--primary-color);
      box-shadow: 0 0 8px var(--primary-color);
    }
    /* Selectbox */
    div[data-baseweb="select"] &gt; div {
      background-color: #27293d !important;
      color: var(--text-color) !important;
      border-radius: var(--border-radius) !important;
      border: 1px solid #44455a !important;
    }
    /* Error message */
    .stException {
      background-color: var(--error-color);
      border-radius: var(--border-radius);
      padding: 16px;
      color: white;
      font-weight: 600;
    }
    /* LaTeX and math formula */
    .latex {
      background-color: #1e1e2f;
      border-radius: var(--border-radius);
      padding: 16px;
      font-size: 1.2rem;
      color: var(--accent-color);
      overflow-x: auto;
      max-width: 100%;
    }
    /* Responsive plot container */
    .plotly-graph-div {
      border-radius: var(--border-radius);
      background-color: var(--card-bg) !important;
      padding: 16px;
      margin-top: 16px;
    }
    /* Helper tooltip */
    .helper-text {
      font-size: 0.9rem;
      color: #c7c7c7;
      margin-top: -12px;
      margin-bottom: 20px;
      font-style: italic;
    }
    /* Section headings */
    .stMarkdown h2 {
      border-bottom: 2px solid var(--primary-color);
      padding-bottom: 8px;
      margin-bottom: 16px;
      color: var(--primary-color);
    }
"""

st.markdown(f"{dark_css}", unsafe_allow_html=True)

# Helper functions

def parse_math_expression(expr_str, locals_dict={}):
    try:
        expr = parse_expr(expr_str, local_dict=locals_dict, evaluate=True)
        return expr
    except Exception as e:
        raise ValueError(f"Could not parse the expression:\n{e}")

def latex_display(expr):
    return f"$$\n{sp.latex(expr)}\n$$"

def solve_equation(input_text):
    """
    Tries to intelligently solve the input equation or system.
    Supports single polynomial equations, trig, exponential, logarithmic,
    systems of equations, and optionally ODEs.
    Input can be equation strings with '=' sign or expressions assumed equal to 0.
    """
    try:
        # Preprocess input for system of equations (comma separated or semicolons)
        systems_delimiters = [",", ";", "\n"]
        for delim in systems_delimiters:
            if delim in input_text:
                eqs_strings = [s.strip() for s in input_text.split(delim) if s.strip()]
                break
        else:
            eqs_strings = [input_text.strip()]

        # Detect variables, support multiple variables
        variables = sorted(list({str(v) for eq in eqs_strings for v in sp.sympify(eq.replace('=', '-(')+')').free_symbols}))
        syms = sp.symbols(variables)

        # Prepare equations list
        eqs = []
        for eq_str in eqs_strings:
            if '=' in eq_str:
                left, right = eq_str.split('=')
                eq = parse_math_expression(f"({left.strip()}) - ({right.strip()})", {str(s): s for s in syms})
            else:
                eq = parse_math_expression(eq_str, {str(s): s for s in syms})
            eqs.append(eq)

        # If single equation, solve symbolically
        if len(eqs) == 1:
            eq = eqs[0]
            solutions = sp.solve(eq, syms if len(syms) &gt; 1 else syms[0], dict=True)
        else:
            # Solve system of equations
            solutions = sp.solve(eqs, syms, dict=True)

        if not solutions:
            return "No solutions found."

        return solutions
    except Exception as e:
        raise ValueError(f"Could not solve the equation(s):\n{e}")

def differentiate_expression(expr_str):
    x = sp.symbols('x')
    expr = parse_math_expression(expr_str, local_dict={'x': x})
    deriv = sp.diff(expr, x)
    return deriv

def integrate_expression(expr_str, definite=False, lower=None, upper=None):
    x = sp.symbols('x')
    expr = parse_math_expression(expr_str, local_dict={'x': x})
    if definite:
        if lower is None or upper is None:
            raise ValueError("Definite integral requires lower and upper limits.")
        integral = sp.integrate(expr, (x, lower, upper))
    else:
        integral = sp.integrate(expr, x)
    return integral

def create_plot(expr_str):
    """
    Create an interactive plot for the expression function of x on domain -10 to 10.
    """
    x = sp.symbols('x')
    expr = parse_math_expression(expr_str, local_dict={'x':x})

    # Lambda function for numeric evaluation safely with numpy
    func = sp.lambdify(x, expr, modules=["numpy"])

    # Generate x values
    x_vals = np.linspace(-10, 10, 500)
    try:
        y_vals = func(x_vals)
    except Exception as e:
        raise ValueError(f"Could not evaluate function for plotting:\n{e}")

    # Clean up y_vals for invalid values for plotly
    y_plot = np.array(y_vals, dtype=np.float64)
    mask = ~np.isnan(y_plot) &amp; ~np.isinf(y_plot)
    x_vals = x_vals[mask]
    y_plot = y_plot[mask]

    # Create plotly figure
    fig = go.Figure()
    fig.add_trace(go.Scatter(x=x_vals, y=y_plot, mode='lines', line=dict(color="#7f5af0", width=3), name=str(expr)))
    fig.update_layout(
        template="plotly_dark",
        title="Function Plot",
        xaxis_title="x",
        yaxis_title="f(x)",
        margin=dict(l=40, r=40, t=60, b=40),
        height=400,
        hovermode="x unified"
    )
    return fig

def show_math_helper():
    st.markdown(
        """
        <div class='helper-text'>
        <strong>Math input tips:</strong><br>
        - Use **^** for powers, e.g. x^2<br>
        - Use `sin(x)`, `cos(x)`, `tan(x)`, `exp(x)`, `log(x)` for functions<br>
        - Use `=`, `/` for fractions<br>
        - Use `sqrt(x)` for square root<br>
        - Multiple equations can be separated by commas or semicolons for systems.<br>
        - For integrals, specify variable as 'x'. Definite integrals require limits.<br>
        </div>
        """, unsafe_allow_html=True
    )

def landing_page():
    st.markdown(
        """
        
        @keyframes fadeInSlide {
          0% {opacity: 0; transform: translateY(-40px);}
          100% {opacity: 1; transform: translateY(0);}
        }
        .landing-intro {
          text-align: center;
          padding: 150px 20px;
          font-family: 'Poppins', sans-serif;
          color: #7f5af0;
          animation: fadeInSlide 2s ease forwards;
          font-size: 3.8rem;
          font-weight: 900;
          user-select: none;
        }
        .subtitle {
          font-size: 1.8rem;
          color: #a3a0ff;
          margin-top: 16px;
          animation: fadeInSlide 3s ease forwards;
        }
        
        <div class="landing-intro">Welcome to MathGenius Pro</div>
        <div class="subtitle">Your AI Math Companion</div>
        """, unsafe_allow_html=True
    )
    # Pause for 3 seconds then clear and continue
    time.sleep(3)
    st.experimental_rerun()  # Reload app to proceed to main UI


# Main application UI
def main():
    st.header("MathGenius Pro - AI Math Companion")

    # Sidebar
    st.sidebar.title("Operations")
    operation = st.sidebar.selectbox(
        "Select an Operation",
        ["Solve Equations", "Differentiate Expression", "Integrate Expression", "Plot Function Graph"]
    )

    show_math_helper()
    expr_input = st.text_area("Enter your expression or equation:", height=100, max_chars=1000)

    if operation == "Integrate Expression":
        definite = st.checkbox("Definite Integral?")
        lower_limit = upper_limit = None
        if definite:
            col1, col2 = st.columns(2)
            with col1:
                try:
                    lower_limit = float(st.text_input("Lower limit (a):", "0"))
                except:
                    st.warning("Enter a valid number for lower limit")
            with col2:
                try:
                    upper_limit = float(st.text_input("Upper limit (b):", "1"))
                except:
                    st.warning("Enter a valid number for upper limit")

    if st.button("Compute"):
        # Clear previous output containers
        output_container = st.empty()
        latex_container = st.container()
        plot_container = st.container()

        try:
            if not expr_input.strip():
                st.warning("Please enter a valid mathematical expression.")
                return

            if operation == "Solve Equations":
                solutions = solve_equation(expr_input)
                if isinstance(solutions, str):
                    output_container.error(solutions)
                    speak(solutions)
                else:
                    output_container.success("Solution(s):")
                    for i, sol in enumerate(solutions):
                        sol_latex = latex_display(sp.Eq(sp.symbols(list(sol.keys())[0]), list(sol.values())[0]))
                        latex_container.markdown(sol_latex, unsafe_allow_html=True)
                    speak("Solutions found and displayed.")

            elif operation == "Differentiate Expression":
                derivative = differentiate_expression(expr_input)
                output_container.markdown("**Derivative:**")
                latex_container.markdown(latex_display(derivative), unsafe_allow_html=True)
                speak(f"The derivative is {sp.latex(derivative)}")

            elif operation == "Integrate Expression":
                integral = None
                if definite:
                    if lower_limit is None or upper_limit is None:
                        st.error("Please provide both lower and upper limits for definite integral.")
                        return
                    integral = integrate_expression(expr_input, definite=True, lower=lower_limit, upper=upper_limit)
                    output_container.markdown(f"**Definite Integral (from {lower_limit} to {upper_limit}):**")
                else:
                    integral = integrate_expression(expr_input, definite=False)
                    output_container.markdown("**Indefinite Integral:**")

                latex_container.markdown(latex_display(integral), unsafe_allow_html=True)
                speak(f"The integral is {sp.latex(integral)}")

            elif operation == "Plot Function Graph":
                fig = create_plot(expr_input)
                plot_container.plotly_chart(fig, use_container_width=True)
                speak("Function plot displayed.")

        except Exception as e:
            st.error(f"Oops, an error occurred:\n{e}")
            speak("An error occurred while processing your input.")

# Using session state to handle landing screen logic on first run
if "show_landing" not in st.session_state:
    st.session_state.show_landing = True

if st.session_state.show_landing:
    landing_page()
    st.session_state.show_landing = False
else:
    main()